List of paradoxes

This is a list of paradoxes, grouped thematically. The grouping is approximate, as paradoxes may fit into more than one category. Because of varying definitions of the term paradox, some of the following are not considered to be paradoxes by everyone. This list collects only scenarios that have been called a paradox by at least one source and have their own article.

Although considered paradoxes, some of these are based on fallacious reasoning, or incomplete/faulty analysis.

Logic

Barbershop paradox: The supposition that if one of two simultaneous assumptions leads to a contradiction, the other assumption is also disproved leads to paradoxical consequences.
What the Tortoise Said to Achilles "Whatever Logic is good enough to tell me is worth writing down...," also known as Carroll's paradox, not to be confused with the physical paradox of the same name.
Crocodile Dilemma: If a crocodile steals a child and promises its return if the father can correctly guess what the crocodile will do, how should the crocodile respond in the case that the father guesses that the child will not be returned?
Catch-22 (logic): A situation where someone is in need of something that can only be had by not being in need of it.
Drinker paradox: In any pub there is a customer who, if they drink, everybody in the pub drinks.
Paradox of entailment: Inconsistent premises always make an argument valid.
Lottery paradox: There is one winning ticket in a large lottery. It is reasonable to believe of a particular lottery ticket that it is not the winning ticket, since the probability that it is the winner is so very small, but it is not reasonable to believe that no lottery ticket will win.
Raven paradox (or Hempel's Ravens): Observing a green apple increases the likelihood of all ravens being black.
Unexpected hanging paradox: The day of the hanging will be a surprise, so it cannot happen at all, so it will be a surprise. The surprise examination and Bottle Imp paradox use similar logic.

Self-reference

These paradoxes have in common a contradiction arising from self-reference.

Barber paradox: A male barber shaves all and only those men who do not shave themselves. Does he shave himself? (Russell's popularization of his set theoretic paradox.)
Berry paradox: The phrase "the first number not nameable in under eleven words" appears to name it in nine words.
Paradox of the Court: A law student agrees to pay his teacher after winning his first case. The teacher then sues the student (who has not yet won a case) for payment.
Curry's paradox: "If this sentence is true, then Santa Claus exists."
Epimenides paradox: A Cretan says: "All Cretans are liars". This paradox works in mainly the same way as the Liar paradox.
Exception paradox: "If there is an exception to every rule, then every rule must have at least one exception; the exception to this one being that it has no exception." "There's always an exception to the rule, except to the exception of the rule—which is, in of itself, an accepted exception of the rule."
Grelling–Nelson paradox: Is the word "heterological", meaning "not applicable to itself," a heterological word? (Another close relative of Russell's paradox.)
Kleene–Rosser paradox: By formulating an equivalent to Richard's paradox, untyped lambda calculus is shown to be inconsistent.
Liar paradox: "This sentence is false." This is the canonical self-referential paradox. Also "Is the answer to this question no?" And "I'm lying."
- Card paradox: "The next statement is true. The previous statement is false." A variant of the liar paradox that does not use self-reference.
- The Pinocchio paradox: What would happen if Pinocchio said "My nose will be growing"?^[1]
- Quine's paradox: "'Yields a falsehood when appended to its own quotation' yields a falsehood when appended to its own quotation." Shows that a sentence can be paradoxical even if it is not self-referring and does not use demonstratives or indexicals.
- Yablo's paradox: An ordered infinite sequence of sentences, each of which says that all following sentences are false. Uses neither self-reference nor circular reference.
Lynch's Paradox: A machine sufficiently "intelligent" to describe its composition and functionality completely is not necessarily self-aware.
Opposite Day: "It is opposite day today." Therefore it is not opposite day, but if you say it is a normal day it would be considered a normal day.
Petronius's paradox: "Moderation in all things, including moderation" (unsourced quotation sometimes attributed to Petronius).
Richard's paradox: We appear to be able to use simple English to define a decimal expansion in a way that is self-contradictory.
Russell's paradox: Does the set of all those sets that do not contain themselves contain itself?
Socratic paradox: "I know that I know nothing at all."

Vagueness

Bonini's paradox: models or simulations that explain the workings of complex systems are seemingly impossible to construct: As a model of a complex system becomes more complete, it becomes less understandable; for it to be more understandable it must be less complete and therefore less accurate. When the model becomes accurate, it is just as difficult to understand as the real-world processes it represents.
Code-talker paradox: how can a language both enable communication and block communication?
Ship of Theseus (a.k.a. George Washington's axe or Grandfather's old axe): It seems like you can replace any component of a ship, and it is still the same ship. So you can replace them all, one at a time, and it is still the same ship. However, you can then take all the original pieces, and assemble them into a ship. That, too, is the same ship you began with.
Sorites paradox (also known as the paradox of the heap): One grain of sand is not a heap. If you don't have a heap, then adding only one grain of sand won't give you a heap. Then no number of grains of sand will make a heap. Similarly, one hair can't make the difference between being bald and not being bald. But then if you remove one hair at a time, you will never become bald. Also similar, one dollar will not make you rich, so if you keep this up, one dollar at a time, you will never become rich, no matter how much you obtain.

Mathematics

See also: Category:Mathematics paradoxes and Paradoxes of set theory

Cramer's paradox: the number of points of intersection of two higher-order curves can be greater than the number of arbitrary points needed to define one such curve.
The infinite sum of alternating integers 1 − 2 + 3 − 4 + · · · can be said to equal 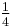$\textstyle\frac{1}{4}$ , which is not an integer.^[2]
Elevator paradox: Elevators can seem to be mostly going in one direction, as if they were being manufactured in the middle of the building and being disassembled on the roof and basement.
Interesting number paradox: The first number that can be considered "dull" rather than "interesting" becomes interesting because of that fact.
Nontransitive dice: You can have three dice, called A, B, and C, such that A is likely to win in a roll against B, B is likely to win in a roll against C, and C is likely to win in a roll against A.
Russell's paradox: Does the set of all those sets that do not contain themselves contain itself?

Statistics

Accuracy paradox: predictive models with a given level of accuracy may have greater predictive power than models with higher accuracy.
Berkson's paradox: a complicating factor arising in statistical tests of proportions.
Freedman's paradox describes a problem in model selection where predictor variables with no explanatory power can appear artificially important
Friendship paradox: For almost everyone, their friends have more friends than they do.
Inspection paradox: Why one will wait longer for a bus than one should.
Lindley's paradox: Tiny errors in the null hypothesis are magnified when large data sets are analyzed, leading to false but highly statistically significant results.
Low birth weight paradox: Low birth weight and mothers who smoke contribute to a higher mortality rate. Babies of smokers have lower average birth weight, but low birth weight babies born to smokers have a lower mortality rate than other low birth weight babies. (A special case of Simpson's paradox.)
Will Rogers phenomenon: The mathematical concept of an average, whether defined as the mean or median, leads to apparently paradoxical results — for example, it is possible that moving an entry from an encyclopedia to a dictionary would increase the average entry length on both books.

Probability

Bertrand's box paradox: A paradox of conditional probability closely related to the Boy or Girl paradox.
Bertrand's paradox: Different common-sense definitions of randomness give quite different results.
Birthday paradox: What is the chance that two people in a room have the same birthday?
Borel's paradox: Conditional probability density functions are not invariant under coordinate transformations.
Boy or Girl paradox: A two-child family has at least one boy. What is the probability that it has a girl?
False positive paradox: A test that is accurate the vast majority of the time could show you have a disease, but the probability that you actually have it could still be tiny.
Monty Hall problem: An unintuitive consequence of conditional probability.
Necktie Paradox : A wager between two people seems to favour them both. Very similar in essence to the Two-envelope paradox.
Proebsting's paradox: The Kelly criterion is an often optimal strategy for maximizing profit in the long run. Proebsting's paradox apparently shows that the Kelly criterion can lead to ruin.
Simpson's paradox: An association in sub-populations may be reversed in the population. It appears that two sets of data separately support a certain hypothesis, but, when considered together, they support the opposite hypothesis.
Sleeping Beauty problem: A probability problem that can be correctly answered as one half or one third depending on how the question is approached.
Three cards problem: When pulling a random card, how do you determine the color of the underside?
Three Prisoners problem: A variation of the Monty Hall problem.
Two-envelope paradox: You are given two indistinguishable envelopes and you are told one contains twice as much money as the other. You may open one envelope, examine its contents, and then, without opening the other, choose which envelope to take.

Infinity and infinitesimals

Burali-Forti paradox: If the ordinal numbers formed a set, it would be an ordinal number that is smaller than itself.
Cantor's paradox: There is no greatest cardinal number.
Galileo's paradox: Though most numbers are not squares, there are no more numbers than squares. (See also Cantor's diagonal argument)
Hilbert's paradox of the Grand Hotel: If a hotel with infinitely many rooms is full, it can still take in more guests.
Pigeonhole Principle: E.g. there must be at least two people in London with the same number of hairs on their heads
Russell's paradox: Does the set of all those sets that do not contain themselves contain itself?
Skolem's paradox: Countably infinite models of set theory contain uncountably infinite sets.
Supertasks can result in paradoxes such as the Ross-Littlewood paradox and Benardete's paradox.
Zeno's paradoxes: "You will never reach point B from point A as you must always get half-way there, and half of the half, and half of that half, and so on." (This is also a physical paradox.)

Geometry and topology

Banach–Tarski paradox: Cut a ball into a finite number of pieces, re-assemble the pieces to get two balls, both of equal size to the first. The von Neumann paradox is a two-dimensional analogue.
- Paradoxical set: A set that can be partitioned into two sets, each of which is equivalent to the original.
Coastline paradox: the perimeter of a landmass is in general ill-defined.
Gabriel's Horn or Torricelli's trumpet: A simple object with finite volume but infinite surface area. Also, the Mandelbrot set and various other fractals are covered by a finite area, but have an infinite perimeter (in fact, there are no two distinct points on the boundary of the Mandelbrot set that can be reached from one another by moving a finite distance along that boundary, which also implies that in a sense you go no further if you walk "the wrong way" around the set to reach a nearby point). This can be represented by a Klein bottle.
Hausdorff paradox: There exists a countable subset C of the sphere S such that S\C is equidecomposable with two copies of itself.
Missing square puzzle: Two similar-looking figures appear to have different areas while built from the same pieces.
Nikodym set: A set contained in and with the same Lebesgue measure as the unit square, yet for every one of its points there is a straight line intersecting the Nikodym set only in that point.
Smale's paradox: A sphere can, topologically, be turned inside out.

Decision theory

Abilene paradox: People can make decisions based not on what they actually want to do, but on what they think that other people want to do, with the result that everybody decides to do something that nobody really wants to do, but only what they thought that everybody else wanted to do.
Apportionment paradox: Some systems of apportioning representation can have unintuitive results due to rounding
- Alabama paradox: Increasing the total number of seats might shrink one block's seats.
- New states paradox: Adding a new state or voting block might increase the number of votes of another.
- Population paradox: A fast-growing state can lose votes to a slow-growing state.
Arrow's paradox: Given more than two choices, no system can have all the attributes of an ideal voting system at once.
Buridan's ass: How can a rational choice be made between two outcomes of equal value?
Chainstore paradox: Even those who know better play the so-called chain store game in an irrational manner.
Fenno's paradox: The belief that people generally disapprove of the United States Congress as a whole, but support the Congressman from their own Congressional district.
Green paradox: Policies intending to reduce future CO₂ emissions may lead to increased emissions in the present.
Inventor's paradox: It is easier to solve a more general problem that covers the specifics of the sought-after solution.
Kavka's toxin puzzle: Can one intend to drink the non-deadly toxin, if the intention is the only thing needed to get the reward?
Morton's fork: Choosing between unpalatable alternatives.
Navigation paradox: Increased navigational precision may result in increased collision risk.
Newcomb's paradox: How do you play a game against an omniscient opponent?
Paradox of hedonism: When one pursues happiness itself, one is miserable; but, when one pursues something else, one achieves happiness.
Paradox of tolerance: Should one tolerate intolerance if intolerance would destroy the possibility of tolerance?
Paradox of voting: Also known as the Downs paradox. For a rational, self-interested voter the costs of voting will normally exceed the expected benefits, so why do people keep voting?
Parrondo's paradox: It is possible to play two losing games alternately to eventually win.
Prevention paradox: For one person to benefit, many people have to change their behavior — even though they receive no benefit, or even suffer, from the change.
Prisoner's dilemma: Two people might not cooperate even if it is in both their best interests to do so.
Relevance paradox: Sometimes relevant information is not sought out because its relevance only becomes clear after the information is available.
Voting paradox: Also known as Condorcet's paradox and paradox of voting. A group of separately rational individuals may have preferences that are irrational in the aggregate.

Physics

For more details on this topic, see Physical paradox.

Cool tropics paradox: A contradiction between modelled estimates of tropical temperatures during warm, ice-free periods of the Cretaceous and Eocene, and the colder temperatures that proxies suggest were present.
The holographic principle: The amount of information that can be stored in a given volume is not proportional to the volume but to the area that bounds that volume.
Irresistible force paradox: What would happen if an unstoppable force hit an immovable object?

Astrophysics

Algol paradox: In some binaries the partners seem to have different ages, even though they're thought to have formed at the same time.
Faint young Sun paradox: The apparent contradiction between observations of liquid water early in the Earth's history and the astrophysical expectation that the output of the young sun would have been insufficient to melt ice on earth.
The GZK paradox: High-energy cosmic rays have been observed that seem to violate the Greisen-Zatsepin-Kuzmin limit, which is a consequence of special relativity.

Classical mechanics

Archer's paradox: An archer must, in order to hit his target, not aim directly at it, but slightly to the side.
Archimedes paradox: A massive battleship can float in a few litres of water.
Aristotle's wheel paradox: Rolling joined concentric wheels seem to trace the same distance with their circumferences, even though the circumferences are different.
Carroll's paradox: The angular momentum of a stick should be zero, but is not.
D'Alembert's paradox: Flow of an inviscid fluid produces no net force on a solid body.
Denny's paradox: Surface-dwelling arthropods (such as the water strider) should not be able to propel themselves horizontally.
Elevator paradox: Even though hydrometers are used to measure fluid density, a hydrometer will not indicate changes of fluid density caused by changing atmospheric pressure.
Feynman sprinkler: Which way does a sprinkler rotate when submerged in a tank and made to suck in the surrounding fluid?
Painlevé paradox: Rigid-body dynamics with contact and friction is inconsistent.
Tea leaf paradox: When a cup of tea is stirred, the leaves assemble in the center, even though centrifugal force pushes them outward.

Cosmology

Bentley's paradox: In a Newtonian universe, gravitation should pull all matter into a single point.
Fermi paradox: If there are, as probability would suggest, many other sentient species in the Universe, then where are they? Shouldn't their presence be obvious?
Heat death paradox: Since the universe is not infinitely old, it cannot be infinite in extent.
Olbers' paradox: Why is the night sky black if there is an infinity of stars?

Electromagnetism

Faraday paradox: An apparent violation of Faraday's law of electromagnetic induction.

Quantum mechanics

Bell's theorem: Why do measured quantum particles not satisfy mathematical probability theory?
Einstein-Podolsky-Rosen paradox: Can far away events influence each other in quantum mechanics?
Extinction paradox: In the small wavelength limit, the total scattering cross section of an impenetrable sphere is twice its geometrical cross-sectional area (which is the value obtained in classical mechanics).^[3]
Hardy's paradox: How can we make inferences about past events that we haven't observed while at the same time acknowledge that the act of observing it affects the reality we are inferring to?
Klein paradox: When the potential of a potential barrier becomes similar to the mass of the impinging particle, it becomes transparent.
The Mott problem: spherically symmetric wave functions, when observed, produce linear particle tracks.
Quantum LC circuit paradox: Energies stored on capacitance and inductance are not equal to the ground state energy of the quantum oscillator.
Quantum pseudo-telepathy: Two players who can not communicate accomplish tasks that seemingly require direct contact.
Schrödinger's cat paradox: A quantum paradox — Is the cat alive or dead before we look?

Relativity

Bell's spaceship paradox: concerning relativity.
Black hole information paradox: Black holes violate a commonly assumed tenet of science — that information cannot be destroyed.
Ehrenfest paradox: On the kinematics of a rigid, rotating disk.
Ladder paradox: A classic relativity problem.
Mocanu's velocity composition paradox: a paradox in special relativity.
Supplee's paradox: the buoyancy of a relativistic object (such as a bullet) appears to change when the reference frame is changed from one in which the bullet is at rest to one in which the fluid is at rest.
Trouton-Noble or Right-angle lever paradox. Does a torque arise in static systems when changing frames?
Twin paradox: The theory of relativity predicts that a person making a round trip will return younger than his or her identical twin who stayed at home.

Thermodynamics

Gibbs paradox: In an ideal gas, is entropy an extensive variable?
Loschmidt's paradox: Why is there an inevitable increase in entropy when the laws of physics are invariant under time reversal? The time reversal symmetry of physical laws appears to contradict the second law of thermodynamics.
Maxwell's Demon: The second law of thermodynamics seems to be violated by a cleverly operated trapdoor.^[4]
Mpemba paradox: Hot water can, under certain conditions, freeze faster than cold water, even though it must pass the lower temperature on the way to freezing.

Biology

Paradox of enrichment: Increasing the food available to an ecosystem may lead to instability, and even to extinction.
French paradox: the observation that the French suffer a relatively low incidence of coronary heart disease, despite having a diet relatively rich in saturated fats.
Glucose paradox: The large amount of glycogen in the liver cannot be explained by its small glucose absorption.
Gray's Paradox: Despite their relatively small muscle mass, dolphins can swim at high speeds and obtain large accelerations.
Hispanic Paradox: The finding that Hispanics in the U.S. tend to have substantially better health than the average population in spite of what their aggregate socio-economic indicators predict.
Lombard's Paradox: When rising to stand from a sitting or squatting position, both the hamstrings and quadriceps contract at the same time, despite their being antagonists to each other.
Mexican paradox: Mexican children tend to have higher birth weights than can be expected from their socio-economic status.
Paradox of the pesticides: Applying pesticide to a pest may increase the pest's abundance.
Paradox of the plankton: Why are there so many different species of phytoplankton, even though competition for the same resources tends to reduce the number of species?
Peto's Paradox: Humans gets cancer with high frequency, while larger mammals, like whales, don’t. If cancer is essentially a negative outcome lottery at the cell level, and larger organisms have more cells, and thus more potentially cancerous cell divisions, you would expect larger organisms to be more predisposed to cancer.
Pulsus paradoxus: Sometimes it is possible to hear, with a stethoscope, heartbeats that can't be felt at the wrist.^[5]
Sherman paradox: An anomalous pattern of inheritance in the fragile X syndrome.
Temporal paradox (paleontology): When did the ancestors of birds live?

Chemistry

Faraday paradox (electrochemistry): Diluted nitric acid will corrode steel, while concentrated nitric acid doesn't.
Levinthal paradox: The length of time that it takes for a protein chain to find its folded state is many orders of magnitude shorter than it would be if it freely searched all possible configurations.
SAR paradox: Exceptions to the principle that a small change in a molecule causes a small change in its chemical behaviour are frequently profound.

Time

Grandfather paradox: You travel back in time and kill your grandfather before he conceives one of your parents, which precludes your own conception and, therefore, you couldn't go back in time and kill your grandfather.
Bootstrap paradox: Can a time traveler send himself information with no outside source?
Predestination paradox^[6]: A man travels back in time to discover the cause of a famous fire. While in the building where the fire started, he accidentally knocks over a kerosene lantern and causes a fire, the same fire that would inspire him, years later, to travel back in time. The bootstrap paradox is closely tied to this, in which, as a result of time travel, information or objects appear to have no beginning.
Temporal paradox: What happens when a time traveler does things in the past that prevent him from doing them in the first place?

Philosophy

Paradox of analysis: It seems that no conceptual analysis can both meet the requirement of correctness and of informativeness.
Buridan's bridge: Will Plato throw Socrates into the water or not?
Chicken or the egg: Which came first, the chicken or the egg?
Fitch's paradox: If all truths are knowable, then all truths must in fact be known.
Paradox of free will: If God knew how we will decide when he created us, how can there be free will?
Goodman's paradox: Why can induction be used to confirm that things are "green", but not to confirm that things are "grue"?
Paradox of hedonism: In seeking happiness, one does not find happiness.
Hutton's Paradox: If asking oneself "Am I dreaming?" in a dream proves that one is, what does it prove in waking life?
Liberal paradox: "Minimal Liberty" is incompatible with Pareto optimality.
Mere addition paradox: Also known as Parfit's paradox: Is a large population living a barely tolerable life better than a small, happy population?
Moore's paradox: "It's raining, but I don't believe that it is."
Newcomb's paradox: A paradoxical game between two players, one of whom can predict the actions of the other.
Paradox of nihilism: Several distinct paradoxes share this name.
Omnipotence paradox: Can an omnipotent being create a rock too heavy for itself to lift?
Preface paradox: The author of a book may be justified in believing that all his statements in the book are correct, at the same time believing that at least one of them is incorrect.
Problem of evil (Epicurean paradox): The existence of evil seems to be incompatible with the existence of an omnipotent, omniscient, and morally perfect God.
Zeno's paradoxes: "You will never reach point B from point A as you must always get half-way there, and half of the half, and half of that half, and so on..." (This is also a paradox of the infinite)

Mysticism

Tzimtzum: In Kabbalah, how to reconcile self-awareness of finite Creation with Infinite Divine source, as an emanated causal chain would seemingly nullify existence. Luria's initial withdrawal of God in Hasidic panentheism involves simultaneous illusionism of Creation (Upper Unity) and self-aware existence (Lower Unity), God encompassing logical opposites.

Economics

Allais paradox: A change in a possible outcome that is shared by different alternatives affects people's choices among those alternatives, in contradiction with expected utility theory.
Arrow information paradox: To sell information you need to give it away before the sale.
Bertrand paradox: Two players reaching a state of Nash equilibrium both find themselves with no profits.
Braess's paradox: Adding extra capacity to a network can reduce overall performance.
Demographic-economic paradox: nations or subpopulations with higher GDP per capita are observed to have fewer children, even though a richer population can support more children.
Diamond-water paradox (or paradox of value) Water is more useful than diamonds, yet is a lot cheaper.
Downs–Thomson paradox: Increasing road capacity at the expense of investments in public transport can make overall congestion on the road worse.
Easterlin paradox: For countries with income sufficient to meet basic needs, the reported level of happiness does not correlate with national income per person.
Edgeworth paradox: With capacity constraints, there may not be an equilibrium.
Ellsberg paradox: People exhibit ambiguity aversion (as distinct from risk aversion), in contradiction with expected utility theory.
European paradox: The perceived failure of European countries to translate scientific advances into marketable innovations.
Gibson's paradox: Why were interest rates and prices correlated?
Giffen paradox: Increasing the price of bread makes poor people eat more of it.
Icarus paradox: Some businesses bring about their own downfall through their own successes.
Jevons paradox: Increases in efficiency lead to even larger increases in demand.
Leontief paradox: Some countries export labor-intensive commodities and import capital-intensive commodities, in contradiction with Heckscher–Ohlin theory.
Lucas paradox: Capital is not flowing from developed countries to developing countries despite the fact that developing countries have lower levels of capital per worker, and therefore higher returns to capital.
Mandeville's paradox: Actions that may be vicious to individuals may benefit society as a whole.
Metzler paradox: The imposition of a tariff on imports may reduce the relative internal price of that good.
Paradox of thrift: If everyone saves more money during times of recession, then aggregate demand will fall and will in turn lower total savings in the population.
Paradox of toil: If everyone tries to work during times of recession, lower wages will reduce prices, leading to more deflationary expectations, leading to further thrift, reducing demand and thereby reducing employment.
Productivity paradox (also known as Solow computer paradox): Worker productivity may go down, despite technological improvements.
Scitovsky paradox: Using the Kaldor–Hicks criterion, an allocation A may be more efficient than allocation B, while at the same time B is more efficient than A.
Service recovery paradox: Successfully fixing a problem with a defective product may lead to higher consumer satisfaction than in the case where no problem occurred at all.
St. Petersburg paradox: People will only offer a modest fee for a reward of infinite expected value.

Perception

For more details on this topic, see Perceptual paradox.

Tritone paradox: An auditory illusion in which a sequentially played pair of Shepard tones is heard as ascending by some people and as descending by others.

Politics

Stability-instability paradox: When two countries each have nuclear weapons, the probability of a direct war between them greatly decreases, but the probability of minor or indirect conflicts between them increases.

History

Georg Wilhelm Friedrich Hegel: We learn from history that we do not learn from history.^[7] (paraphrased)

Notes

^ Eldridge-Smith, Peter; Eldridge-Smith, Veronique (13 January 2010). "The Pinocchio paradox". Analysis 70 (2): 212–215. doi:10.1093/analys/anp173. ISSN 1467-8284. http://analysis.oxfordjournals.org/cgi/content/short/70/2/212. Retrieved 23 July 2010.
As of 2010^[update], an image of Pinocchio with a speech bubble "My nose will grow now!" has become a minor Internet phenomenon (Google search, Google image search). It seems likely that this paradox has been independently conceived multiple times.
^ Euler, Leonhard (1768). "Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques". Memoires de l'academie des sciences de Berlin 17: 83–106. http://www.math.dartmouth.edu/~euler/docs/originals/E352.pdf. "... quand on dit que la somme de cette série 1 - 2 + 3 - 4 + 5 - 6 &c. est ¼, cela doit paroitre bien paradoxe"
The quote from page 84 translates as "...when it is said that the sum of this series 1−2+3−4+5−6 etc. is ¼, that must appear paradoxical"
^ Newton, Roger G. (2002). Scattering Theory of Waves and Particles, second edition. Dover Publications. p. 68. ISBN 0486425355.
^ Carnap is quoted as saying in 1977 "... the situation with respect to Maxwell’s paradox", in Leff, Harvey S.; Rex, A. F., eds (2003). Maxwell's Demon 2: Entropy, Classical and Quantum Information, Computing. Institute of Physics. p. 19. ISBN 0-7503-0759-5. http://web.archive.org/web/20051109101141/http://vlatko.madetomeasure.biz/Papers/maxwell2.pdf. Retrieved 15 March 2010.
On page 36, Leff and Rex also quote Goldstein and Goldstein as saying "Smoluchowski fully resolved the paradox of the demon in 1912" in Goldstein, Martin; Goldstein, Inge F. (1993). The Refrigerator and The Universe. Universities Press (India) Pvt. Ltd. p. 228. ISBN 9788173710858. OCLC 477206415. http://books.google.com/books?id=R3Eek_YZdRUC. Retrieved 15 March 2010.
^ Khasnis, A.; Lokhandwala, Y. (Jan-Mar 2002). "Clinical signs in medicine: pulsus paradoxus". Journal of Postgraduate Medicine (Mumbai - 400 012, India: 49) 48 (1): 46. ISSN 0022-3859. PMID 12082330. http://www.jpgmonline.com/text.asp?2002/48/1/46/153#Pulsus%20paradoxus:%20what%20is%20the%20paradox?. Retrieved 21 March 2010. "The “paradox” refers to the fact that heart sounds may be heard over the precordium when the radial pulse is not felt."
^ See also Predestination paradoxes in popular culture
^ Hegel, Georg Wilhelm Friedrich (1832). Lectures on the Philosophy of History.